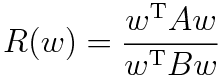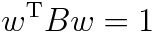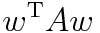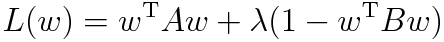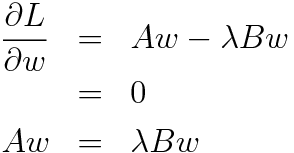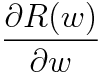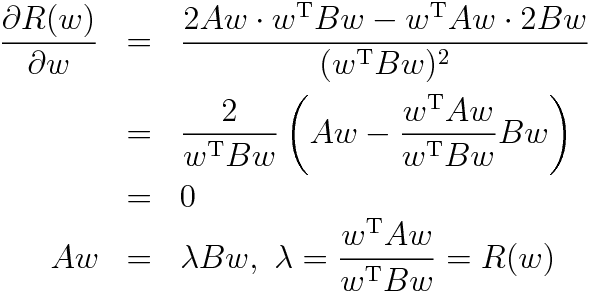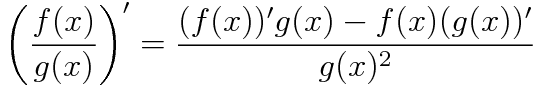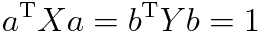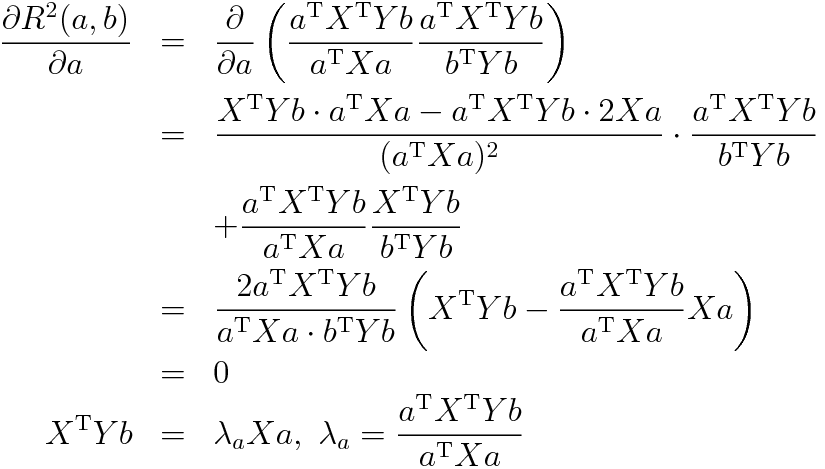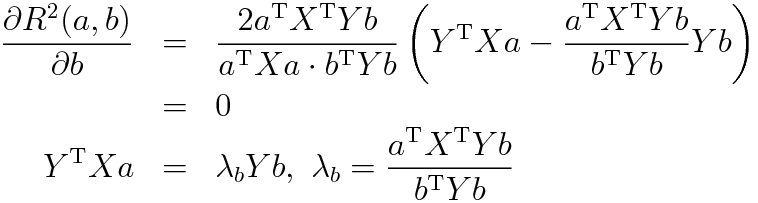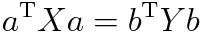レイリー商と一般化固有値問題
Rayleigh Quotient and Generalized Eigenvalue Problem
2011/08/23 i-horse
主成分分析や判別分析及び正準相関分析ではレイリー商として知られる形の式を最大・最小にするようなベクトルを求めることを考える。
レイリー商は行列A,B及びベクトルwを用いて
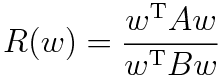
と表される。
ここでこのレイリー商が極値を取るようなwを求めることを考えるが、巷の多変量解析の教科書では制約条件を加えて計算を簡略化している。
すなわち
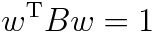
という条件のもとで
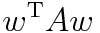
が極値を取るようにしようというのだ。
この根拠はwは二次形式として分母分子にあるので定数倍の自由度がある。
だから制約条件を設けることでその自由度を消してやる。
これよりラグランジュの未定乗数法を用いることで
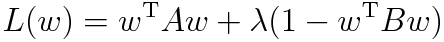
となり結局
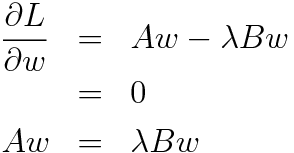
という一般化固有値問題に帰着される。
これが定石であるのだが実はこの制約条件というのは本質でなく外すことができる。すなわち直接
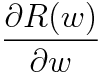
という偏微分を考え式変形すると
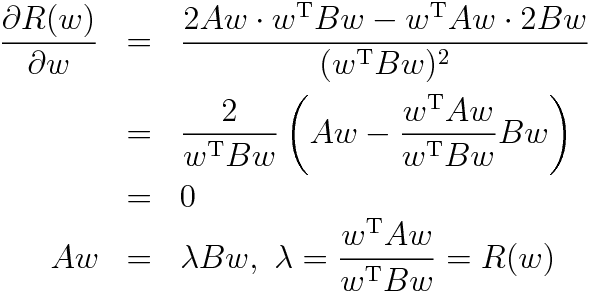
(参考:商の微分法)
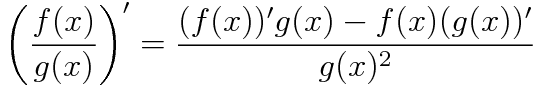
となり結局同じ一般化固有値問題に帰着されるのだ。
こちらのほうが簡単ではないだろうか?
ちなみに正準相関分析では

のような商を最大化することを考える。これはレイリー商と似てはいるが違うものである。ここでも定石は
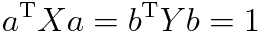
という制約条件をつけて考えるのだが、これも直接偏微分すれば一般化固有値に帰着されるだろう。しかし平方根の微分はめんどくさいので二乗の偏微分を考えることにする。この操作によって解が変わることはない。
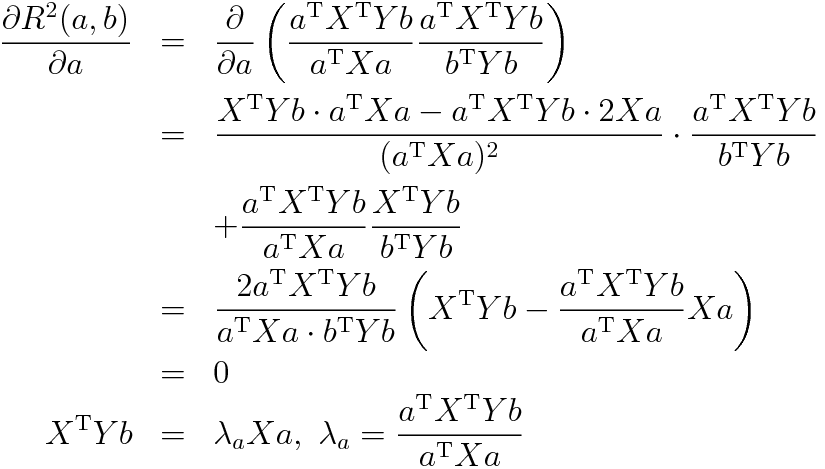
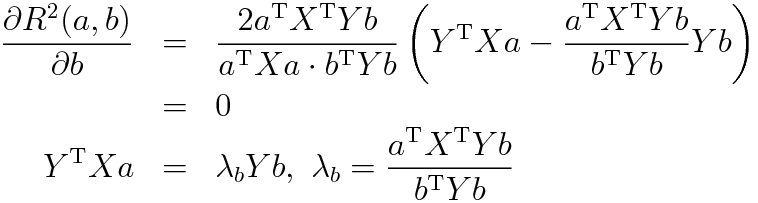
となり
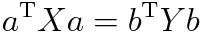
と置けば結局正準相関分析に付随する一般化固有値問題に帰着されることがわかる。
実は行列ノルムに関しては次のようなことが示されるので以上の結果は当然とも言える。

ざっと