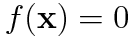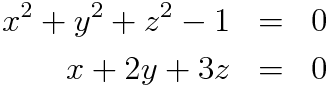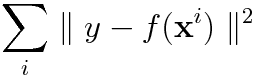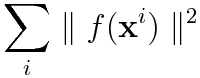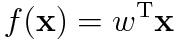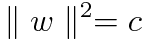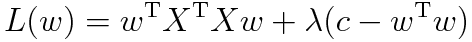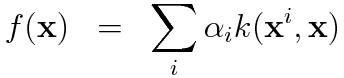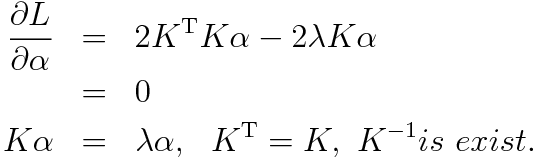観測データからの高次元空間を制限する陰関数推定手法について
A Method for Extraction Implicit Functions which Restrict High Dimension Space from Observed Data
2011/08/24 i-horse
--abstract--
高次元空間を制約する陰関数を推定する手法が実は主成分分析の裏返しになっていることを示す。
--key word--
Implicit Function, Principal Component Analysis, Kernel Principal Component Analysis
画像などの高次元データを考える際、それを扱いやすいような低次元に圧縮する手法が様々に知られている。例えば主成分分析はデータの情報エントロピーを最大にするような低次元に圧縮する手法である。また画像であればDCT変換などによってスパースなデータに変換した後圧縮センシングの手法により圧縮及び再生が可能である。
データが圧縮可能であるということは観測している対象が高次元空間を自由に動けるわけでなく何らかの多様体上に制限されていると考えられる。例えば主成分分析では超平面上に制限されている場合に有効であるし超平面に限らない多様体に制限された場合に有効であるISOMAPやカーネル主成分分析なども知られている。
しかしこれらの手法ではデータが多様体上でどのように分布しているかを得ることはできるが、その多様体が高次元空間中でどのような形をしているかを知ることはできない。もちろん主成分分析では超平面を張る基底ベクトルを得ることができるがISOMAPやカーネル主成分分析など非線形に拡張すればわからなくなってしまう。
そこでデータが多様体上でどのように分布しているのかではなくデータが分布している多様体がどのような形をしているのかを推定する手法を考えてみたいと思う。一般的な多様体を表現することは難しいのでここでは多様体が陰関数の形で定義されていると仮定する。すなわち
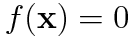
という恒等式によって記述されていると仮定する。例えば三次元中に埋め込まれている円は例えば
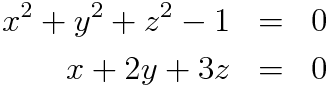
のような陰関数によって記述されている。
では実際にデータ集合が与えられたときにそれが埋め込まれている多様体を記述する陰関数を求める手法を考えてみよう。一般に関数を推定する統計的枠組みとして回帰分析というものが知られている。例えば関数に線形性を仮定すれば線形回帰、非線形に拡張した場合にはカーネル回帰というものがある。陰関数の推定についても回帰分析における目的変数をすべて0とおいた場合と考えることができる。つまり回帰分析においては以下のような二乗誤差を最小にするような写像を求めることを考えるが
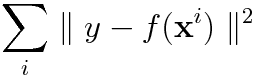
陰関数の推定を考えるとこの目的変数を0と置くことで
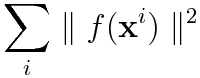
を最小化するという問題に帰着できることがわかる。以下では関数が線形を満たす場合を考える。すなわち
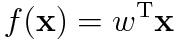
とかける場合を考える。ここでこの評価関数を最小にするような自明な解はもちろんw=0であるがこれを除外するために
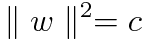
と置くと(c は定数)ラグランジュの未定乗数法によりラグランジュ関数は
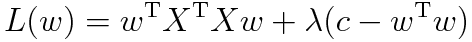
とかけその極値は

という固有値問題により求まる。すなわち固有値λを最小(もしくは0)にするような固有ベクトルwが求める写像に対応するのだ。
実はこれは主成分分析と全く同じ計算をしていることになる。主成分分析は上記の固有値問題において固有値λを最大にするような固有ベクトルwによってデータを低次元空間に射影する手法であった。陰関数推定によって求まるwはこれらのベクトルと直行している、すなわちデータが存在する超平面の法線ベクトルに対応していると言える。いままで主成分分析をしていた際に使わずに捨てていた小さい固有値に対応する固有ベクトルは実は陰関数推定に対応していたのだ。陰関数推定はまさに主成分分析のホルモンである。
次に写像を非線形写像にまで拡張しよう。具体的にはカーネル回帰分析を用いる。この時写像は
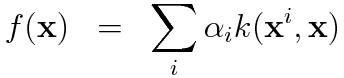
のようにかけ線形の場合と同じ理由により係数が0でないという制限を設けると二乗誤差を最小にするような係数はラグランジュの未定乗数法により求めることができ、ラグランジュ関数は
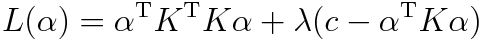
となり(ただしKはグラム行列)その極値は
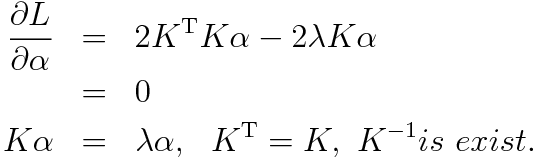
という固有値問題を解くことにより得られる。これもカーネル主成分分析と全くおなじになっており小さい固有値に対応する固有ベクトルが陰関数推定の結果、大きい固有値に対応する固有ベクトルがカーネル主成分分析に対応する結果となっている。
以上にみるように高次元空間中に埋め込まれた多様体を記述する陰関数を推定する手法を考えると回帰分析を通して主成分分析・カーネル主成分分析と対応していることがわかった。
ざっと